Category: Taught Courses

Courses i have taught or am teaching.

How to do math?

Subir / / Calculus-1

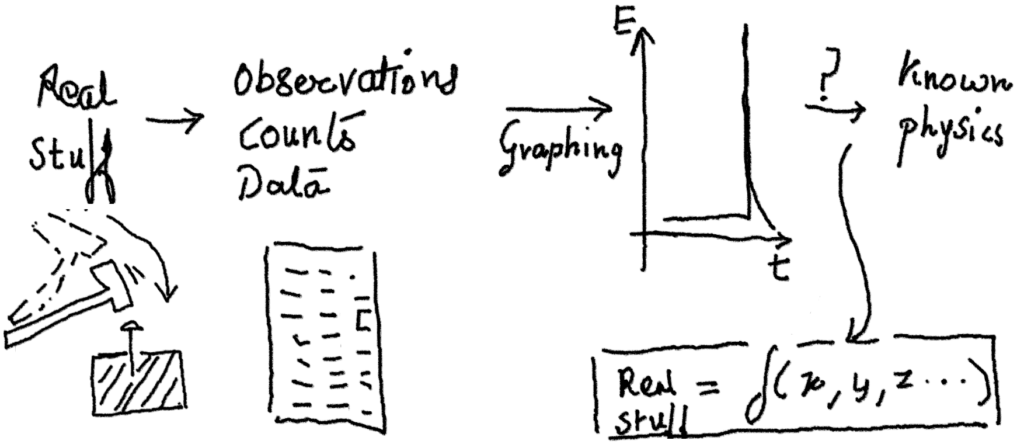
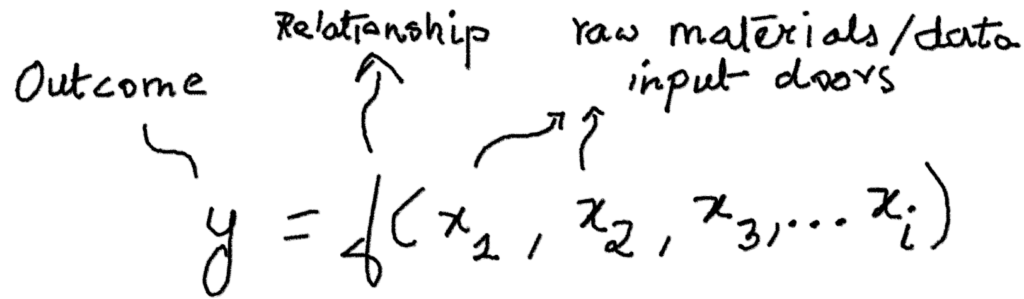
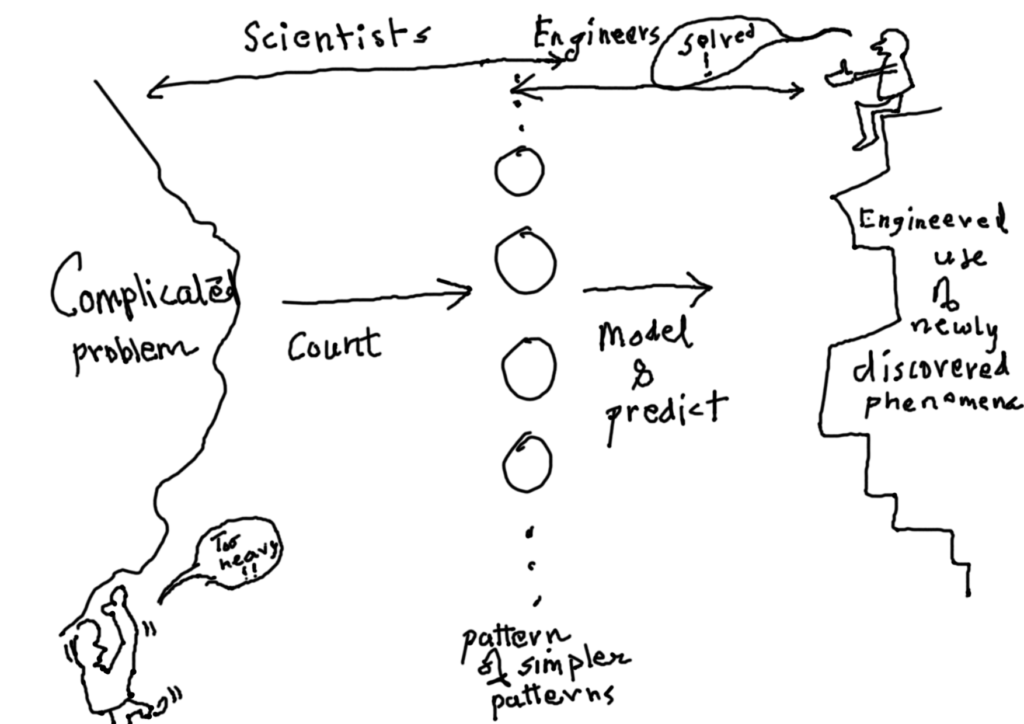
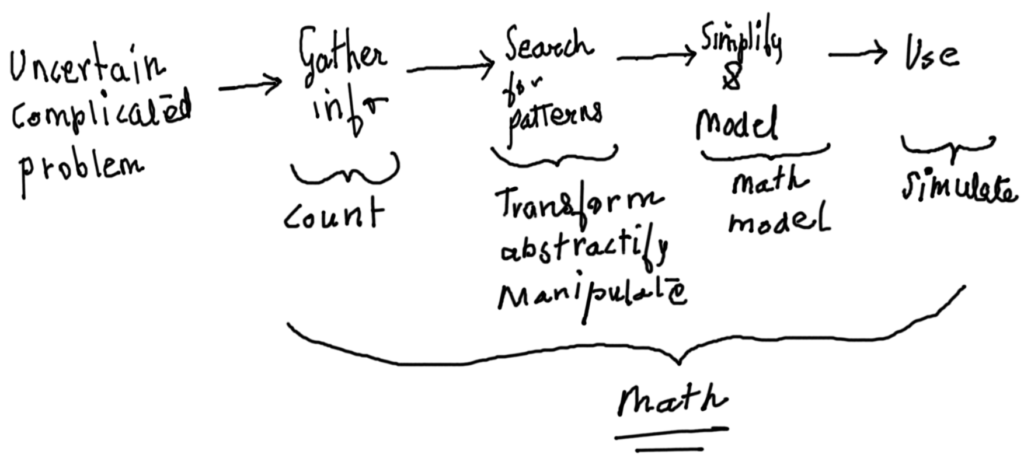
As seen in the previous posts (What is math to us? and What is a function?), math is relevant and practical, at the least. It is the means through which humans can comprehend the world in a definite manner, with more and more evolving ability to objectify and count complicated phenomena. But as a student of math, how can we act on math, like in day-to-day terms? I suppose the overall scheme is:

  • Observe and count
  • Make good tables with one to one or sequential coorelations between various parameters which were counted/observed/measured.
  • Plot the numbers in various graphs.
  • Transform the number tables through known mathematical manipulations to form better graphs so that we head towards relating the unknown to the knowns.
  • Strive toward the ‘equation form’ of representation, which can link the known and the unknowns through a simple textual code – the model.
  • Use the ‘model’, to test the model and fine-tune, specify regions where the model works and where it doesn’t.
  • Next, use the well tamed model to extrapolate the future or link up with other models.
  • Use this model as a potential modular component, a brick to build a conceptual house so to say, to understand the next new phenomena and repeating again all the previous steps.

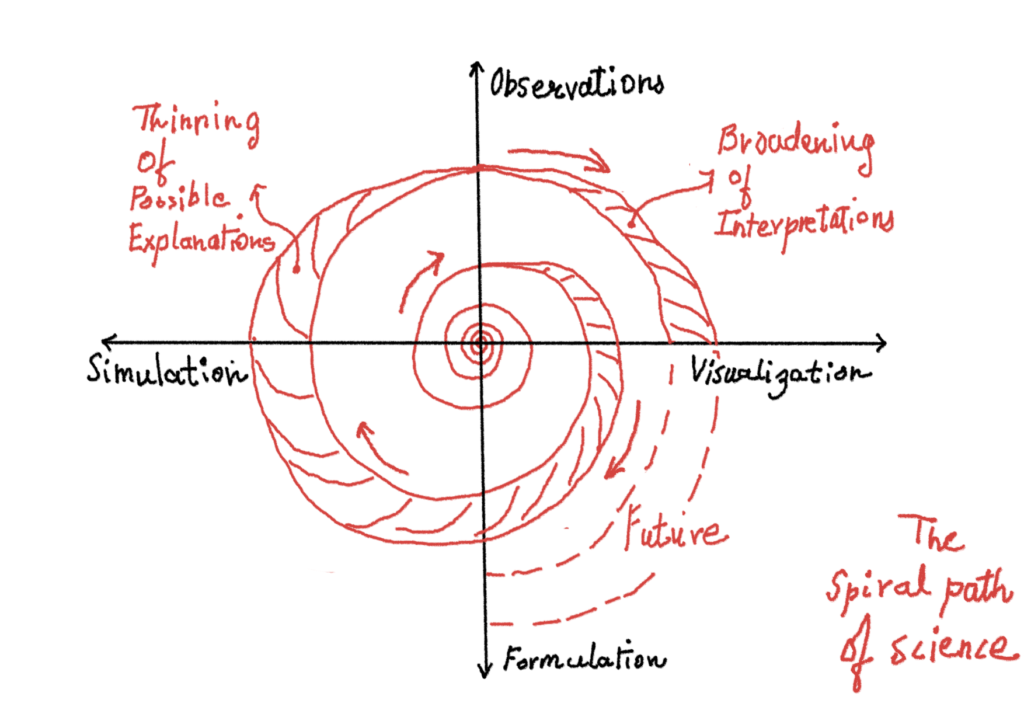
The list above could be represented by an illustration as a spiral path of science. Here one begins by observations and makes multiple interpretations of it. Some of these interpretations form various kinds of ‘interesting’ graphs and also include some manipulation of the observed data to form different and more revealing graphs (Visualization). These graphs are then broken and tamed with graphs of known functions and eventually a textual formula or model is formed (formulation). These sets of models are used to create simulated replicas of the real phenomenon and then compared with the reality (Simulation). The broadening path indicates the many ideas and possible interpretations one begins with. But when one tests the simulations against reality, a lot of ideas are forced to be dropped from the realm of scientific thought as as they don’t satisfy the simulation=reality test, thus narrowing the path again culminating at the observation arm of the axes. At this stage, when the simulation becomes a well proven model, it could be used to further interpret or predict newer observations, as depicted by the increasing size of the spiral.

Why is representing data in a graph so important?

This is a good question, an i can only wonder some answers here which obviously are very naive due to the lack of sufficient thought or experience or training in the domain of mathematics. I am thinking the role of vision in our lives. The ability to sense at a distance is crucial to the survival of so many animals, including humans. With that sense-at-a-distance ability, it also needs to be good enough to interpret fast, if the remote scene is friendly or otherwise. And how do we do that? Our vision systems (sight+brain) has learnt that some patterns are good, some are bad and so in the remote scene we search for these cues. We search for patterns which are similar to what we have known so far. Our pattern seeking behavior is crucial to everything. Not all pattern knowledge is first hand. That is probably where culture, education, traditions, etc come in. But let’s not digress.

So our pattern seeking vision is kind of super trained to remove the clutter and get to sections of the scene which resemble what we have known previously through either extension/exaggeration (points depicting a line) or creative manipulation (Zodiac signs of astronomical bodies?). However, not all information is visual in nature, for example the changes in temperature over time. In fact much of the information is not instantaneous – the domain where vision works (Einstein would disagree a bit here, arguing that nothing is instantaneous. But lets escape that trap for now through a classical way.). So what graphical representation does is probably transform the significant amount of non-instantaneous information, spread over tables and tables of measured data into an instantaneous form (2D image), so that our well developed ability to figure out visual patterns within a noisy scene can come in handy.

So shouldn’t we stop here?

Why do we need algebra?

So although graphs made out of tabulated data do reveal a lot, often we are in need to transform the data to obtain more revealing graphs. Example could be a real data showing if x occurs with some magnitude, event y also occurs with some magnitude.

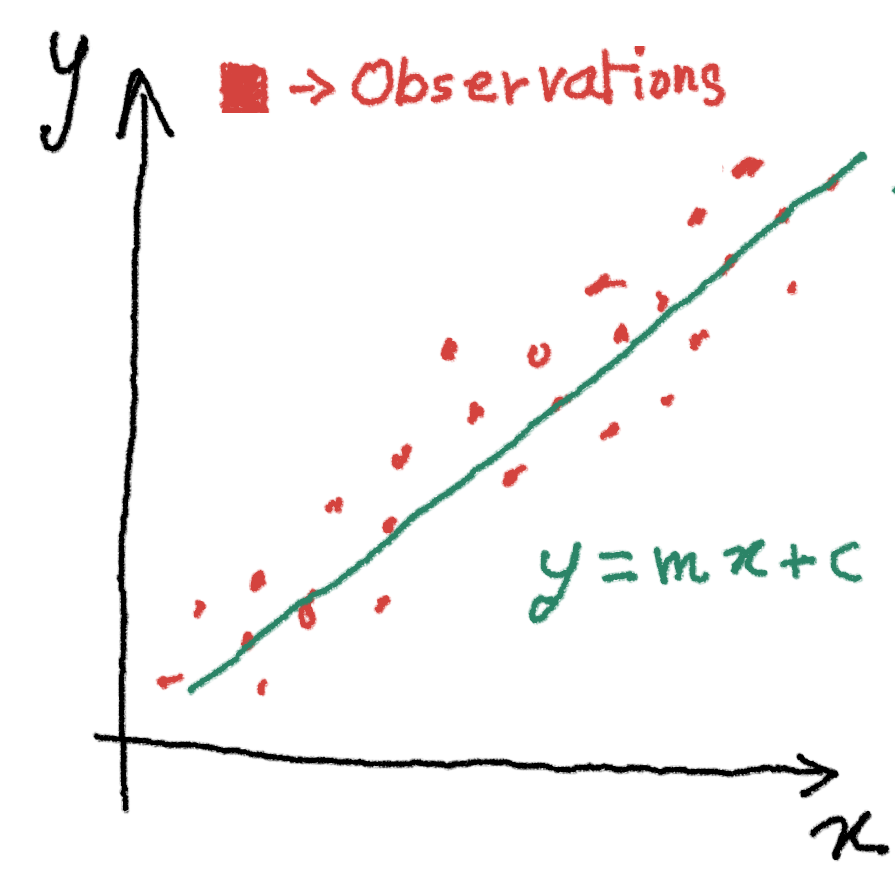
However, the observations always have some noise in them, like in the image above. Yet, knowing that Y is growing when X is growing, the observed data could be further simplified, by just doing compromises on the accuracy of the model and representing the reality instead by a simple equation.

Another good example of why an equation is helpful more than a graph is when using measurement instruments. A common way to measure temperature is through a RTD (Resistance Temperature Detector) the electrical resistance of which varies as temperature changes. This changing resistance can be measured through an electronic circuit and the temperature can be interpreted. But how? Often the RTD resistance to temperature curve is one measured through real experiments, where the resistance is recorded (y-axis) for an increasing temperature (x-axis). This curve is not a straight line. When using this device in real circumstances, 2 approaches can be used. The real experimental values (the table of resistance Vs temperature) for each degree change in temperature could be stored in a computer and any real resistance measurement can be checked against these values to get an accurate temperature. However this method will need a lot of digital data storage space and many operations. Another method is to convert the graph into a polynomial equation which has only one input and one output, the resistance measured and the temperature, respectively. Storing this simple equation and evaluating it in a small space constrained computer is much easier and safer. Although the polynomial does not exactly match the real measured curve, it remains suitable for most practical purposes. (More on this here).

Where to begin?

The first tools to learn is tabulation and tabular operations. What better thing invented for this purpose than the spreadsheet! The advantage of the spreadsheet is that it could be used to store tabulated data, manipulate it by transformations, graph it, and and even simulate formulae into graphs.

A good base to learn spreadsheets could this.

And a good tutorial for graphing and analyzing data here.

What’s a function?

Subir / / Calculus-1

Seriously, what are functions? We have been forced to learn what functions by definition are in our previous math courses all through school life. Bu i never understood of used those definitions in real life situations? Or not that simply as shown in the text books. So, what do we mean by funcitons?

In our daily parlance, we do use this word function as if the action associated with a tool, for example. Lets say a hammer, what is its function? Due to its design and heavy strong metal weight and the end of a long rod, when it is set into moving and obstructed by a rigid block of wood, the poor nail which comes in the way is subjected to immense forces as it is the only thing resisting the motion of the heavy metal weight brought to a sudden progressing stop! Thus, what is the function of a hammer? A tool to transfer significant amount of mechanical energy, in one direction, at a point B, lets say. But the more human question is, why bother writing it this way or that? A hammer works, why scratch our brains when we have already achieved a good tool? Probably because, if you have been given an industrial situation where you need to hammer 1000s of nails on a wooden box production line, and achieve good finish, without using much energy, its in these cases you need to understand the physics of a simple hammer so that an optimized hammering system could be made!

Thus, as discussed in the previous post, the abstractification of real phenomenon, such as a hammer, helps us reduce the complicated reality into a table of numbers. And when that reduced data is available, one can search for a complete understanding of it, by comparing it with known and well understood phenomena, such as the concepts of force, inertia, etc – via creating a function that connects or maps the real data with complicated components to a combination of known physics.

And when a real phenomenon is mapped to known physics via a newly created custom function, this custom function can then be optimized for any particular need. The same function could be used to design a machine to punch thousands of small depressions in a jeweler’s gold punching machine or be used to punch out holes in thick walls. It becomes a versatile tool! Though this process is the scientific process, the other process also exists where one learns as one goes and through intuition ‘gets’ the function embedded in experiential learning. The debate between these two processes is very interesting and has an interesting example – the contrast between Tesla and Edison. Such is the important role a function plays in our scientific method. But what does a function actually contain?

Imagine a sunflower seed. It has all the important information it needs to grow into a plant. No matter what amount of water, soil, nutrients, etc you give or not give, the seed will only and only produce the sunflower plant and not a mango tree. So a function is like a seed, it has all the information to reproduce a version of reality contained in itself, and all it requires are external supply of numbers. In other words there are 3 components to a function – input variables or doors to allow numbers to come in, relationship between inputs from various doors, and the resultant output plant or reality, written in mathematical form as :

The functional form of a plant will be contained in a seed in the form of DNA. A crop of sunflowers could be a result of many factors such as rain, temperature, humidity, pests, density between seeds, soil contents, etc. If a function of a crop of sunflower could be made, it could help in optimizing water consumption for example by accurately computing the amount of water required daily to keep crops healthy. Currently farmers do not have a mathematical function at their disposal. As we will see, it is not easy to ‘model’ real phenomena into simple cozy functions, but that is the pursuit of science.

There is a catch in the above. Can the same quality and quantity of inputs, be it the seed quality, the environment, the water, the soil, etc be the same and yet the output differ? If this were to be true, then it only means we have failed to form a good valid function. The same set of inputs must give the same set of outputs. This is the requirement of the mathematical definition of functions. However, different set of inputs can give the same set of outputs! For example, different amounts of water varied as per different atmospheric humidity could produce the same quality of sunflower crops. In fact this is the key to optimization problems we will see in future posts.

Can we explore the above chain of thoughts on other day-to-day aspects? Examples:

  • Function of a bicycle
  • Ceiling fan
  • Switch
  • Smartphone

What is math to us?

Subir / / Calculus-1

Why do we math? What is the role of math in our society, in our day-to-day lives? Even after using math in many ways, i don’t have a clear answer. I wonder why students would respond to these questions. It may be that there will be follwing responses:

  • I don’t know.
  • I like math, but i never thought of it as useful.
  • It is used in economics and stock market and scientific research?
  • Artificial Intelligence or data sciences?
  • …

We might know instances where and when the tiger has been spotted, but we don’t know the tiger. So the question, why do we math?

To me, the pretext lies in humanity’s difficulty in dealing with uncertainty. If you don’t know when it will rain, you can’t sow your seeds because it will then be exposed to the birds and insects which might eat them up! Or how much time we could expect the sun to be in the sky? Or, how much of material which i need can i take in return for other materials which i have surplus? Imagine the early humans who began to worry about the uncertainties like the above. How would they deal with these, day in, day out. No one has the luxury to be born to a super rich family which ensures there are no uncertainties. In fact, the super rich worry about the uncertainty of their fortune and so are back in the same loop – how to make certain what is uncertain?

One core idea, which rests the human mind to a certain extent is that of patterns. Imagine a brick house, the bricks being the unit which was repeated in multiple ways to make the house. The idea that patterns exist in our world and the universe is so relieving! The sun’s time in the sky repeats day in day out. A known amount of grains give out a known amount of crops when planted. An object thrown up falls down, and that too if its thrown up in a certain fixed way, it falls down after a fixed time! This trick is the key.

With patterns, it may have been possible to the early humans to make simple this complicated scary world. They came to know that all these complications can be reduced to replications and combinations of smaller things. For example

house = x*bricks + y*cement + x*man-hours + other bits.

Now each thing, there could be seen as something to do with patterns which are repeated and combined with other patterns to make something complicated. Had this trickery not been discovered, there would be no brick houses. We would still be searching for a nice soft rock or twigs to make our nests. The implications of knowing or not knowing that patterns exist, could be severe. Can it be said that all knowledge is that of our eternal quest for patterns? Patterns we have discovered or perceive or are yet to discover?

But does a discovery of a pattern only have an emotional benefit aspect to it? No. We do something more – we make newer patterns from it for our other needs. A reference could be made here to an earlier blog post on Stereotyping Vs Prototyping that discusses our stereotyping tendency (fit everything into limited diversity of patterns). Making newer patterns, to add to our library of patterns, could be called as prototyping. We make models with a newly discovered pattern. When Newton and others came up with simplified mathematical form of the motions and bodies of the world, others rushed to use these simple representations of patterns to predict motion of astronomical objects, or for guessing the energy required to move objects vertically across a building and so on. So these patterns become models – tools which can be used.

So what’s math got to do with all this pattern business? Well, math is basically counting. Why do we need to count and what is that? One way to put it is to account for something big and complicated by repeating something small and simple in so many counts. For example, you wish to move a table through a door. One way is to haul the heavy table and through trial and error see if it can get past the door with a few iterations. Another wiser way is to count the door dimensions as multiples of your palm width, and then do the same for the table. After you note these down, you can then simplify these further, and figure out which orientation of the table with respect to the door can achieve what you set out for. So the abstractification of the problem helps our mind to process, imagine, draw and basically manipulate known information (dimensions of the door and table) to illuminate the unknown (how to get one across the other). That is the essence of basic math.

An example could be language. If someone’s speaking to you in sounds, how can you convert that into something you understand? So, typically you would record it – meaning count the intensity/volume of the person over a span of time. Then you would see if certain sound bytes correspond to the finger pointing of the person to certain fixed objects. This is searching for patterns. Then when you know say ‘debbidabbypoo’ corresponds to ‘run’ and ‘haletkaletpichkao’ corresponds to ‘You’ then you create a model sentence to test your interpretation on to the other person, something like ‘haletkaletpichkao debbidabbypoo’. This model will then be put on test and if the person runs away, you have a working model (and a lost sample)! But this is risky, you would like to learn first how to tell the person to come back before you ask it to run away. Now you see you are manipulating the situation to your benefit, also called taming the model. Similar things happen in all sorts of problems, and math is this tool that can help quantify, patternize, model, and simulate based on counting numbers and abstracting.

Teaching math?… wha?

Subir / / Calculus-1

So i have to teach a basic calculus course at the SSLA this coming semester. Tense? Sure! Why? I’v never done this before (… biting my nails). If you are a potential student of mine seeing this post, i would like to assure you that I am a bit handy with calculus. But yes, the thing to worry about is that i am nowhere near as practiced or proficient as a good teacher should be! And also that teaching is an art, not everyone’s cup of tea. But i’m learning that art, so please bear with me. The way i do it, or like to do it is to experiment and co-learning.

Worries apart, i wonder what should be the role of a teacher in such a class? Or put in another way, what transformation should the participants have after going through this class? Or even more basic, what should basic calculus mean to anyone? I am not clear about the former 2 questions, but for the latter i can imagine the following possibilities:

  1. Make oneself a fanatic about advanced math and calculus :- This could happen when the subject becomes an end in itself. Like math nerds on auto mode! This is far too ambitious. And i fear i won’t do any justice to the kids in this domain. Not in this lifetime.
  2. Embodying calculus :- when the subject has utility value as well as philosophical value in such a way that you can begin to see its terminology and ideas relevant to understanding your day to day life.
  3. Calculus as a no-brainer tool :- when its just like a car. Key in from some place you are not happy with, and you could drive it to a happy place, without worrying about how the engine works. Like a ‘black-box’ tool.
  4. Calculus as a certificate :- A key document respected by the society! It implies that one has spent enough time and effort to bottle up enough information which everyone knows will be drained once done with the exams. The optimists however hope that some of it will remain as nostalgic residues for years to come.
  5. ” I Quit !”

Personally, i have had a lot of content in #4s, and sadly i can vouch for their uselessness. But i have also had the opportunity of being around point #3 during my projects work, and have learnt to appreciate it as a great tool. But with this 3 month elective course (thanks to Sumithra Surendralal – my friend and a wonderful science and math teacher from the SSLA who suggested i try it out this semester) i will upgrade a bit to region #2, i hope. And with the students, I hope they carry away at the end of the course some of the joys (#2) and utilities(#3) of basic calculus. And i hope that i would help my kids steer clear of #5.

Design for COVID-19

Subir / / Maker Culture 2

Review of problems:

  • Social
    • How to deal with isolation?
    • Whats the plan next?
    • Where are the leaders?
    • Where is the nearest COVID-19 test center?
    • How to know what is truth and what’s a rumor?
    • Community
      • How can i contribute to the community by being at home?
      • Who’s caring for the elderly?
      • Who’s caring for the homeless and family-less people?
      • Is there a food-bank where i can contribute?
  • Technical
    • Lack of good reusable face-masks
    • Lack of sufficient protective clothing for healthcare professionals
    • Is there a disinfectant for general home use? Without chemicals?
    • Medical
      • Where is the cure?
      • How can we increase testing? What’s the bottleneck?
      • How can i improve my immunity so that i could be resilient to complications if I get infected?
  • Economy and future
    • How will the economy behave next?
    • How can i work from home and still earn?
    • I am in the manufacturing sector, there cant be ‘work-from’home’option!! What can i do?
    • I am not digital-literate. What can i do to earn?

Focus of Maker Culture class

For completion of course, one needs to note the following:

  • Making hardware is NOT mandatory.
  • Making an online documentation of problems and solutions is mandatory. All evaluations will be based on single blog which contains:
    • CA1 essay as a separate blog post.
    • CA2 blog posts on skills learnt and its story.
    • CA3 blog post.

What is CA3?

Make a blog-post in your regular blog answering the following questions. You can break the following into multiple blog posts. The total marks for CA3 is 20!!!

  • Study a specific problem due to COVID-19 outbreak: (4 marks)
    • Why this problem has appeared?
    • What’s the social angle to its origin and possible solution?
    • What is the impact of the problem?
  • Study existing solutions to the problem: (4 marks)
    • Conventional solutions used before the outbreak.
    • New ideas/innovations in response to the outbreak.
    • Limitations of all these solutions. Example:
      • Not customized for Indian use, or for use in my city.
      • Too costly.
      • Still in research stage, not yet commercialized.
      • Too unreliable for common use.
      • No service in my city.
  • Your personal take on the problem: (8 marks total)
    • Technically, what device you can imagine can solve the problem.
    • What is the nearest existing design that you like and would base your innovative solution on?
    • Your design (5 marks!):
      • Specify the challenges you would like your design to ultimately meet – the ultimate design criteria!
      • Make hand sketch to explain the concept of your design.
      • Make a TinkerCAD model of how the device will look.
      • If your design has electronics in it, describe how the electronics will help.
    • List skills and materials required for your design. Also called the BOM (Bill of Materials).
    • How will you make it? What tools will you use, what skills you will need to learn.
  • Pitch your idea in the form of a ppt presentation (4 marks).
    • Why you want to solve this problem?
    • Who would you like to solve it for?
    • What is the problem with existing machines/ideas?
    • What challenges your design can address?
    • Explain your design briefly?
    • Can you make a plan of making it?

What problems?

  • A reusable germicidal face-mask – with UV treatment of inhaled and exhaled air.
  • A disinfectant box that can UV disinfect any object like clothing, shoes, phone, money, etc.
  • An automatic hand wash unit to be placed in public places.

#15 Intro to 3D printing

Subir / / Maker Culture 2

So, didn’t do posts inbetween from #9 till now since i was lazy and it seemed that not much philosophical depths the hand skills training carried out in the previous classes could be written about unless backed by enough photographs and illustrations which would have called for extreme dedication on my part. So a summary rather:

  • In electronics, we began experimenting with LEDs and how to wire them up in the correct way and in the not correct ways. We saw, willing or otherwise how LEDs can be damaged if a resistor is not used. Interestingly we have some LEDs in our stock which has some form of inbuilt circuitry that A) prevents them from blowing up even without a resistor (though it gets hot) B) Red, green and blue colors in single LED in sequence (else it would have been a white LED) and C) The colors switch automatically as if programmed in that way.
  • Next all kids were asked to recreate the first alphabets of their names on a breadboard, learning in the process the breadboard basics. But this was the first time the question was posed: how to connect a bunch of LEDs to one another but lit by a single battery?
    • Series and parallel connections were tried out as experiments and it was concluded that in series connections, there’s a limit as to how many LEDs can be lit up. If connected in series, meaning positive leg of first LED to the positive of a 9V battery and the negative leg connected to the positive leg of another LED, this kind of connection was first tested out. Suppose all LEDs were of red type, each LED drops 1.5V by default. So how many would fit in to cover 9V? So, 1.5V times 6 = 9 that means at the max 6 LEDs could be lit up in series!
    • However, in a parallel connection all positive legs are joined together and connected to a 9V battery via a resistor while all the negative legs are joined together to meet the negative of the battery. Even if each LED drops 1.5V, since its in parallel the 1.5V across all remains the same irrespective of how many LEDs are connected. Its a bit abstract or maybe i am not taking effort to explain well, either ways its better than series connection. This was established experimentally.
  • Next, the kids were asked to construct their alphabets on a zero PCB. This involved learning a bit about the soldering gun, how to join the legs together, put jumpers across when continuous path construction using solder itself as molten wire was not possible, etc. This took some time because this is really a kind of skill. After many faithfully constructed their letters, some lit up, some didnt and it was kind of bitter sweet experience. But due to lack of time we move ahead.
  • The idea of Arduino as a small programmable computer was introduced. Initally the LED on board was played with. Then it was time to connect an external LED and do the blinking and fading examples. The fading code was explained and kids played with the timings. The next test was to use fading on the alphabets kids had made, which worked quiet easily!
  • While the above session dealt with Arduino’s output capability, in another session the idea of analog signals and its measurement was discussed. Due to my own ill-planning i made a huge mess as to how to deliver this sligthly abstract but very important concept across. It was a mess and the kids were bewildered unnecessarily because i asked them to simulate different voltages using voltage dividers and so on with some formulas and stuff. Totally un-called for. I rather could have arranged for some analog sensors like LDRs and stuff to illustrate analog measurements!

Now we come to 3d printing.

The obvious questions that one would ask in general:

  • Why make something in the first place?
  • What are the ways of making things?
  • If we have all the ways of making things then why invent more? What situations make conventional making techniques obsolete or difficult?
  • What is 3d printing and how it works?
  • When did it all began and how is it relevant today?

The above questions in themselves need 1 session or atleast half of it. But we dont have that luxuary as we need to begin on the projects as soon as possible. So i will skip all that and do the following:

  • What is 3D printing?
  • Make a shape on tinkerCAD online.
  • Export it to Cura for slicing
  • See the wonder while it gets printed.

So first to set the context of making, what are the conventional ways?

  • Joining, using existing shapes and getting them together through gluing or welding, etc.
  • Subtractive processes such as sculpting, turning, milling, etc.
  • Additive processes such as brick laying, 3d printing, etc.
  • Moulding and casting, such as all engines, etc.

So we could illustrate 3d printing by an actual look at how the layers are formed line by line. I think that should be enough to replace any words from anyone.

The remaining is plain discovery mode with some assistance and letting things evolve.

#9 Intro to electronics (continued)!

Subir / / Maker Culture 2

Last time we saw some analogies between Pune traffic and electronics.

  • Imagine its 8AM on a weekday. The IT parks and companies and schools and what not feel a very desperate need for some people to come over and occupy their seats and so some work so that the organizations could sustain and hopefully make some money to live out their lives (yes organizations behave as self-serving organisms!). On the other hand the people residing in Kothrud for example feel some form of similar desperation to reach in the required zones (organizations) in time so that they may be able to live happily ever after. The requirement of both groups for each-other exist purely for their own satisfaction, irrespective of higher goals, mostly. Also one does only care for the other as far as their survival is concerned, and nothing more.
  • Now at 8AM, the mobile group makes this whole drama to get into their cars and bikes and buses and move over to the awaiting arms of the organization, all at the same time because its convenient for all organizations and people to work synchronously in a city, why – i don’ t know. Its just like that i guess. Anyways, all these lacs of people moving about from one end of the city to another, criss-crossing each other, this road or that road, non-linear paths, honking and exchanging pleasantries to as many one can find involved in similar goodness – all for the sake of meeting the desperation of both the organizations and individuals.
  • On the way the mobile group bumps into fixed or moving objects, creating vibrations to both the interactive parties. Most of the times they don’t bump in, nevertheless the pressure of reaching a certain place in time and uncertainty of road ahead cause frantic adjustments in the movements, keeping everyone in an alert dynamically changing state. If the dynamic state is essential to the flow of this group.
  • Also the roads are too important on the way!! Pune has nice roads, except many are under perennial construction and especially with the synchronized mobility choose to attain a life of their own. And they also have some rough surfaces, all in the best interest of the mobility (used here like ‘ nobility’ ) so that they don’ t slide off too quickly or reach their destinations before time!!! So these roads too modify the movement of the people, taking toll on their energy and draining it as the humbum and noise of the traffic. The noise and mystery of traffic jams pass on to other members of the mobility way way remote from the starting point of jams, as if reflection has taken place.
  • Sometimes, bikers in Pune decide enough is enough and discover new roads no one knew ever existed. If a pioneer discovers a part, a whole group of ardent followers are developed within a fraction of a second following the path of their true leader until they find another leader opening another path for them. Who says we have no leaders, we have plenty, only they are busy discovering paths on the blocked roads!
  • And then there are the mandated traffic signals that try to regulate the different current flows into different paths, keeping one flow from obstructing other flow and avoiding traffic jams. Pune’s bikers however know with mysterious precision when a signal need not be taken seriously, like total stop or total start, especially during peak hours. This infact has a new effect that the traffic never stops completely, just varies in speed through a signal, everyone just adjusting to each-other so much so that the traffic remains optimized all the time, even while criss-crossing at right angles! What a splendid example of an ecological balance!
  • There are one way streets where only a few obey the direction while the others obey their perception of dynamic directions. However these streets do help maintain and distribute traffic in certain ways.
  • Also there are dividerless roads in plenty where opposite moving traffic interact almost while touching their counterparts, the line between them having a life of its own. When a signal is in force, the bikers and cars crossover the divider lines and huddle up as if the watching a signal turn green is the most interesting sight they will ever seen in their lives!
  • While the people move about, their movement creates an immense effect on the sides of their paths. New shops and restaurants and vehicle repair workshops crop up, catering to this mind-boggling every day activity thousands are involved in. While some of that immense activity is just the useless noise and confusion and humbum, there is a significant part of it that is useful for another ecological activity – the roadside business. So any traffic movement can be associated to carry with it the side forces that help carry on the movement.
  • Somtimes the reverse happens. A immense roadside activity attracts non-desperate people to move over from far off places to these roadside places, leading to another form of ecological movement.
  • Most importantly, many companies to which these people move to survive on the manufacturing the mode of transport required for their movement. Kind of a self-serving cycle of events, feeding into one another.

The above could just be the case of electrons (people). The desperation being the voltage, the number of traffic size being the current, the roads and obstructions being the resistance, the signals being the transistors. The huddling up or swelling of traffic at a signal or slow road being the capacitor effect. One way street being a diode and so on. A more conventional and beautiful explanation is given in this video:

Once explanations are out of the way, we could proceed to some experiments. The ideas is what activity one can do that will A) Excite and B) Inform? The former is especially important since after the previous explanations their minds would have totally gone switch-off and so that needs to be revived.

  • Lets begin with a diode. What is a diode and why it is important could be explained. Give students an LED each and ask them to look at it. Also observe some aspects of it, especially the leg length. Explain them the concept of current flow, and how high current could damage the diode. How does a diode gets damaged?
  • How to restrict the current? Give them the largest resistor, and make them figure out the resistance of the resistor. Color codes and all.
  • Connect all of them in the set direction, so that things glow of not glow with the battery one.
  • Now change the resistance and see what happens.
  • Explain the concept of bread board, to ease the process.
  • Explain the concept of a multimeter to ease the process.
  • Can you add switches to the circuit so that its not always on and save battery?

#8 Part 2 – Basic electronics

Subir / / Maker Culture 2

A general question would be to probe and bring out what the students already know about electronics from the deepest and farthest corners of their minds.

  • electrons exist and move around
  • Oh and they can move in certain directions together too.
  • But why move in certain direction? what fun in all this? – While moving, the desperation of moving can be used to get some output.
  • This desperation can be measured – called Voltage
  • How many electrons are desperate can be called current
  • But if so many desperate people wish to move to a certain direction, can they all move in one go? What if the road is narrow? or if the bus is old? or if there’s no road!!
  • We could explain a little bit of welding here, because of the stool making workshop.
  • But there’s something that makes the voltage and current not independent of each other!! – Mr. Ohm comes in here. How can one explain resistance? Toll booth could be a nice example or a police checkpoint or Pune Metro?
  • What happens at a traffic jam? Frustration and boredom, equivalent to the heat created in a wire due to resistance.
  • Now what if too much traffic is let go on a narrow road? Too much jam/heat at the bottleneck = fights and bursting of the road down. If on both sides there is water, the traffic is stuck, else it will find paths and try to make new roads – the same as it happens on a circuit board where chaos reigns can keeps life interesting (many first hand experiences) 😉
  • But why moving so much traffic from one place to another? What use? Traffic movement implies its an important road. Construct a nice one, build some hotels and shops, and make money. In electronics this could be making some work done by human manipulators.
  • Like traffic, the electrons can be made to go about many circles in the city before it can cross the city to its destination. All the while adding to the chaos, the heat of the city, the jams, etc. But all this activity leads to businesses of buses and cars, of shops and stuff. The potential difference of distance between home and office divided by the manipulative city (load) inbetween with manipulators (politicians, bureaucrats, companies, etc ) constantly trying to get the best out of desperate citizens.
  • One old Mr. Lorenz and Mr. Maxwell figured out how to convert the side drift effect (businesses and viewership and consumerism) that moving traffic produces to make engines! Like our economy, if there’s no traffic between distant places the local market will be saturated and wont be able to harness the energy to drive or grow economy. The current and magnetism analog could be extended further, but that’s enough for now.
  • So how can electrons/people be manipulated?
    • The simplest is make a road and put a toll booth on it – the resistor.
    • Then vary the toll opening and closing to get variable traffic flow.
    • Then pass this traffic over a small diaphragm to make some sound – a beeper or make some light.
    • A transistor could be the use of some traffic to affect the flow of another traffic route, or to use a police man to switch on or off a traffic flow or control it ever more slightly – a transistor!
    • Capacitor?
    • Inductor?
    • Diode? – thats easy – a one way street.
    • Switch – a gate like thing, like on a toll booth.
    • Heater – a large road with too much traffic to flow through it…

#8 Part 1 – Documentation

Subir / / Maker Culture 2

So far we have seen the following:

  • How humans have been makers all the way
  • How making is the in thing now with technology and how technology itself works.
  • We saw why modern way of organized large scale mass manufacturing leaves a whole bunch of population deprived of the benefit of technology because of economics.
  • With a guest lecture we saw how the city we live in is driven top-down of what and how a city should develop, not concerning the citizens’ opinions itself but that of corporates and non-native glamorous ideas – big money!
  • We have also began in a workshop making things for a change – the mainstay of this course.
  • Now, over the time we have also collected problems we face first hand in small hand written notes.

Assignment #1 (CA1) is almost over and i am correcting the submissions. Stupid me i asked the poor students to write 2.5k words each on the topic of how technology plays a role in A) World politics B) Nature C) Rich/poor economic divide D) Gender divisions and E) In our intimate personal lives. Many did a fabulous job, and its a real pleasure to read from the fresh young passionate minds here. I guess these kids should be the teachers and we the old ones should learn to be their students and followers!

Given all this recap, where to now? OK what we will head to is here:

  • Some electronics basics with a little theory and then some burning stuff.
  • Some modern making tools like 3d printers
  • And projects

But before we go to the above it will be important to discuss the boring subject of documentation. I know this is really not my thing, i do it sometimes, but most of the times its in my head and if i happen to have an accident or something and am alive after that but minus the memories – all is gone. Not that there’s much worthwhile in there but a lot of journeys were the bricks of mistakes and failures could make a solid pyramid.

Why we document? A boring question, but if we really ask this and ponder on it its worthwhile. Documentation is an act of casting memory, thoughts and experiences into something that will last longer. Why do we wish to make something last? A typical Society and Science type open-ended question this one. Would be interesting to get student’s views and discussions on this. A simple answer from my simple mind is – so that we may not repeat it, again! How we run away from repetitions in this case is very interesting in contrast to how we run towards repetition when it comes to rituals and traditions. So a little more poking can reveal a better answer – so that we can avoid the cognitive burden of repeating mistakes. Now rituals and traditions fall into place as there are no mistakes there, just the apparently proven, ages old techniques to hang on to for safety.

Often one encounters the notion that its stupid to reinvent the wheel. So very common, i have been at the receiving end of it numerous times. Although documentation can help prevent reinventing the wheel kind of situations, its nevertheless should not be made an excuse. Reinventing the wheel is essential for learning – artists begin by mimicking the work of masters, artisans and apprentices do the same. So do scientists and engineers. Its utter crap, this idea of avoiding reinventing the wheel. It is a must despite knowing that mistakes have been documented. But facing the mistakes first hand gives a huge dimension to our experiences – the expectation of an outcome totally falling on its face and the emotional commotion at that moment, not knowing what went wrong and what to do next. This going through the fire of mistakes (literally firey moments for many makers), catapults oneself to a significant experiential height. Coming back to documentation, reading past documentation on one hand and dealing with the humiliating defeat in front of nature makes a wonderful revelation often. It is then that the documentation of the past fits right into the cavity of the moment, the mind red hot prepared and all. So this way first hand experience and learning from n-th hand sources go hand in hand.

However, not always the experiements we do is exactly repeatable like the ones described in words of the past. The past works only can give a gist, the remaining must form an unfathomable experience only to be retained and lost forever after life’s down. Every maker makes new experiences, even if the experiment and work is the same. And there can be so many variations in the experience that if everyone chooses to write down and document, still its all worth it. This documentation of 1st hand info is one of the most valuable thing that differentiates us from the animals. In our short lifespans, its equivalent to living 1000s of years, just because we could read and contemplate a little of the documentations of the past. And thanks to this beautiful property of nature – repeatabilty, we can build from where others have left off, or even choose to go back and build from an 100 year old version!

Another advantage of documentation is for self-reference, within a lifetime. We’ll be doing many things, and will be forgetting many things. But somethings if we document, we take the pains to sit and write, kind of parking the ideas somewhere to be referred to in future, we that isn’t a bad thing is it? Often when i am asked about my projects, i point them to this site and makes my and the asker‘s job easier. I write here to clear my mind before class and also so that i could look back and see if i made sense. Sometimes some students may use some of this shit for some referencing or pointing out how dumb that teacher was 😉

In short, we should begin somewhere, so that’ll be the task tomorrow. To make a blog and post photos and videos of our projects and works and assignments for posterity.

#5 and #6-7

Subir / / Maker Culture 2

#5 was a guest lecture by Mr. Khaliq Parker on the new wave of ‘smart’cities being driven by the government. Khaliq discussed various aspects of what it means to by a good city to live in, what we the citizens are aware of and not aware of while continuing to live in Pune for example. Then the discussion headed on to what we wish to change in Pune, a ‘Smart’ city itself. On this basis it was further discussed is we are aware of the technological interventions in this city which have already been initiated by the smart cities mission and so on. And finally the main point of having such a discussion within the maker course context was to see if the ‘makers’ could either ride on the government initiatives or form parallel citizen science initiatives of their own to arrive at a much more organic base-up development model for an urban area.

#6-7 were a stool making workshop conducted on the 26th of January 2019 at our maker friend Mr. Sandipan’s place. We wanted to make about 5 steel and wood tall stools, wooden seat and metal legs. We got all the materials and began at about 8:30 in the morning and completed only 2 by the end of the day at 8:30 in the evening. 2 batches of students, 8 each participated in this workshop and i guess they had lot of fun actually handling some tools. They used a jig-saw to cut plywood to make a form that could be used to arrange and weld metal pieces in a designed geometry. Then they cut some metal, arc welded some of these + some polishing and so on. Some students could begin working on the wooden steats, which were basically some trunk of a tree.

There’s so much scope to explore and do, so i hope we could repeat the above workshop and finish all the stools with decent looks. Fingers crossed!!