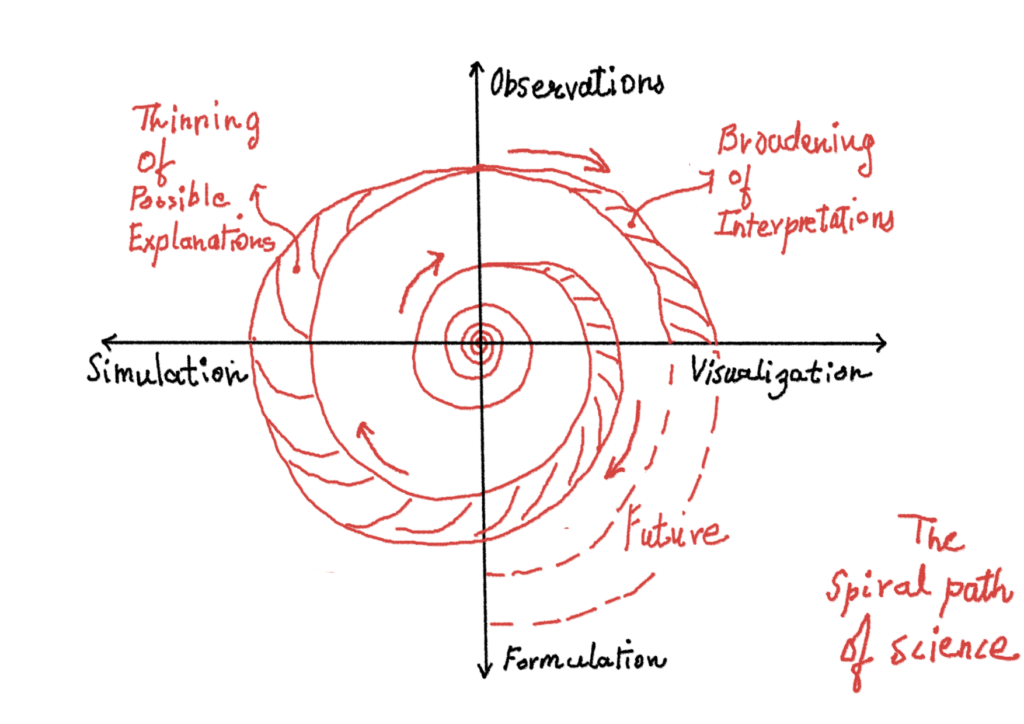
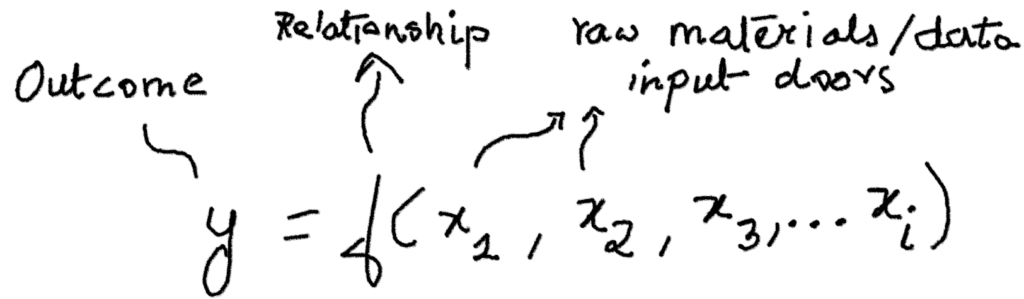
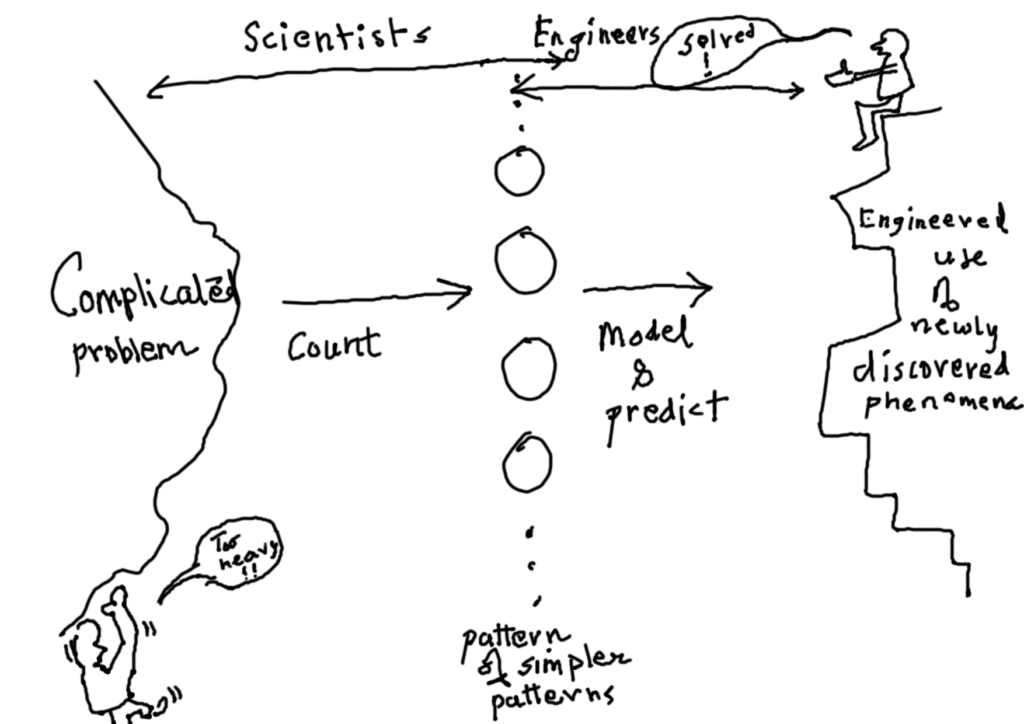
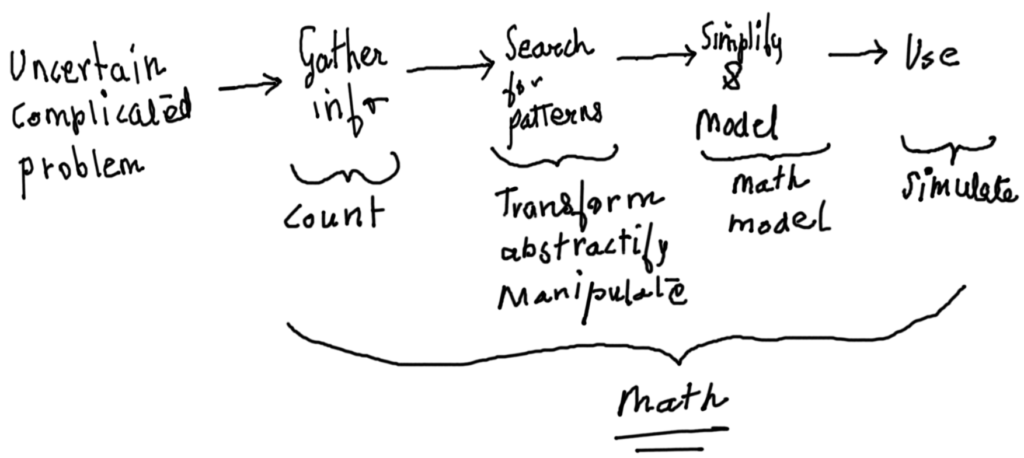
I have been a teacher on and off for over the past few years. I have taught about making devices/instruments, some maths and some physics to undergrads at a local elite college in Pune. I have had a mixed experience if I reflect back. The last year was particularly intense and tough on me, and so I have decided to quit formal teaching, at least for a year.
Being a normally driven person with some excitement in what I do, I tend to get carried away expecting the same from others. This was evident in some projects I had given and mentored with kids. Everything started nicely, and the kids responded well. These kids weren’t from the engineering or the sciences base, but studied a mix of various subjects from humanities and some science and mathematics. They loved the initial joy of making gadgets and were quite enthusiastic to make new things and imagine new things to be made. We learnt some electronics, soldering, 3d printing, design tools, etc. After learning some basic skills they were tasked to practice those skills in making projects, from a list of projects I needed help in. Although the projects started well, I realized the kids loosing steam half way through. Except a few, most failed to push enough and complete the individual targets set for their particular projects. They weren’t also coming back to me with their issues or discussing among themselves, I felt. As a teacher passionate about the projects and this whole act of making things by hand, I was disturbed. Even after repeated coaxing, the apathy of some of the teams was evident. And my annoyance in this lack of effort or sincerity probably became more and more evident. One of the students even complained that she could not communicate her challenges with me, or do the work assigned to her for her own exams, because I was “rude” apparently. By the end of the course, only a small group actually completed their projects, the rest completed the formalities of the course.
Another example was from teaching maths and physics. Most students showed interest and participated in the class with great amount of passion. I think I fared better in these classes as a teacher than in the maker classes. In another course where I was to co-teach research methods, I realized the similar trends – loss of interest by students as the work got harder. While these phenomena were on going, where students at one point may find traction in the course, while on the other side of the calendar loose interest, I realized I as a teacher also converted from a hopeful and compassionate human at the beginning of the calendar to a hard task master at the end of the course. While this is not black and white, it seemed so one of the perspectives shared by my colleagues. What was evident were the hard comments I was giving back on submissions by students, calling out callousness and shoddy work, calling out blatant plagiarism, abuse of technological privileges such as AI tools. My hard comments disturbed the kids, and the concerned authorities/teachers/admins. The sad part was that I was not so aware of this until it was brought to my notice by my colleagues.
When I re-read my own written comments, I realized that they were mean. I was shocked myself, and felt embarrassed. Some of my words could be interpreted as severe and not acknowledging the person’s struggle or the overall context. I have struggled to understand these reactions of mine, often finding all the fault with me on one hand and repenting it. Sometimes I feel that I was too passionate about the subject and expected very highly of the students, which may have led me to be so harsh on their performance. As a teacher this has been the toughest of all experiences. I also feel I was under much stress of teaching. Facing a class full of judging youngsters, my personal anxiety of ‘performing’ as a knowledgeable guide while i struggled with the nuances of the topic, my lack of experience in the teaching the subjects and other reasons may have led to a built up of emotions, which manifested in my uncalled for expressions. The critical feedback I received from about a year of passionate effort from my end, came as a shock. It was disheartening to say the least. I am still processing the experiences and interpretations, not completely sure what went wrong, what was right, etc. The moral burden of being on the ‘wrong’ or unkind to people, especially kids is crushing. But I learnt a lot I would say, and I am still discovering layers and layers within this rich experience. I loved many moments of the teaching experience, and especially the joy of connecting with kids via the topic on hand, mutually participating in the wonders of the subject, and so on. It gives me hope that I was not too bad a teacher or a human, most of the time.