Seriously, what are functions? We have been forced to learn what functions by definition are in our previous math courses all through school life. Bu i never understood of used those definitions in real life situations? Or not that simply as shown in the text books. So, what do we mean by funcitons?
In our daily parlance, we do use this word function as if the action associated with a tool, for example. Lets say a hammer, what is its function? Due to its design and heavy strong metal weight and the end of a long rod, when it is set into moving and obstructed by a rigid block of wood, the poor nail which comes in the way is subjected to immense forces as it is the only thing resisting the motion of the heavy metal weight brought to a sudden progressing stop! Thus, what is the function of a hammer? A tool to transfer significant amount of mechanical energy, in one direction, at a point B, lets say. But the more human question is, why bother writing it this way or that? A hammer works, why scratch our brains when we have already achieved a good tool? Probably because, if you have been given an industrial situation where you need to hammer 1000s of nails on a wooden box production line, and achieve good finish, without using much energy, its in these cases you need to understand the physics of a simple hammer so that an optimized hammering system could be made!
Thus, as discussed in the previous post, the abstractification of real phenomenon, such as a hammer, helps us reduce the complicated reality into a table of numbers. And when that reduced data is available, one can search for a complete understanding of it, by comparing it with known and well understood phenomena, such as the concepts of force, inertia, etc – via creating a function that connects or maps the real data with complicated components to a combination of known physics.
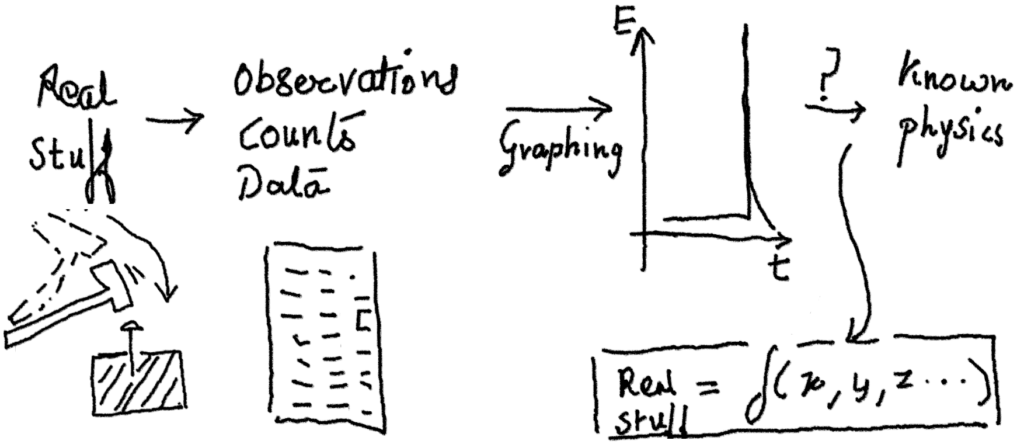
And when a real phenomenon is mapped to known physics via a newly created custom function, this custom function can then be optimized for any particular need. The same function could be used to design a machine to punch thousands of small depressions in a jeweler’s gold punching machine or be used to punch out holes in thick walls. It becomes a versatile tool! Though this process is the scientific process, the other process also exists where one learns as one goes and through intuition ‘gets’ the function embedded in experiential learning. The debate between these two processes is very interesting and has an interesting example – the contrast between Tesla and Edison. Such is the important role a function plays in our scientific method. But what does a function actually contain?
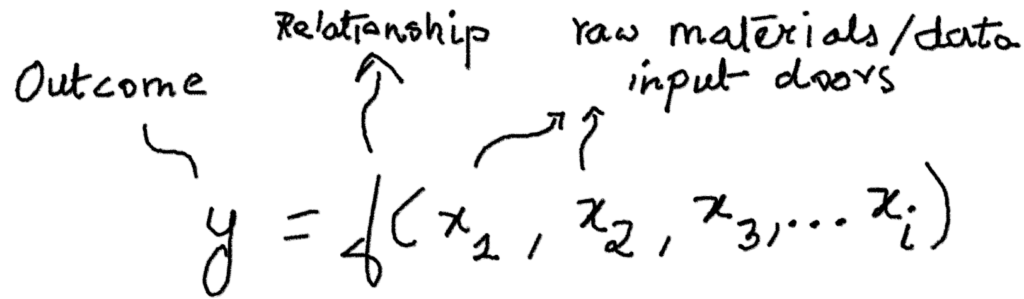
Imagine a sunflower seed. It has all the important information it needs to grow into a plant. No matter what amount of water, soil, nutrients, etc you give or not give, the seed will only and only produce the sunflower plant and not a mango tree. So a function is like a seed, it has all the information to reproduce a version of reality contained in itself, and all it requires are external supply of numbers. In other words there are 3 components to a function – input variables or doors to allow numbers to come in, relationship between inputs from various doors, and the resultant output plant or reality, written in mathematical form as :
The functional form of a plant will be contained in a seed in the form of DNA. A crop of sunflowers could be a result of many factors such as rain, temperature, humidity, pests, density between seeds, soil contents, etc. If a function of a crop of sunflower could be made, it could help in optimizing water consumption for example by accurately computing the amount of water required daily to keep crops healthy. Currently farmers do not have a mathematical function at their disposal. As we will see, it is not easy to ‘model’ real phenomena into simple cozy functions, but that is the pursuit of science.
There is a catch in the above. Can the same quality and quantity of inputs, be it the seed quality, the environment, the water, the soil, etc be the same and yet the output differ? If this were to be true, then it only means we have failed to form a good valid function. The same set of inputs must give the same set of outputs. This is the requirement of the mathematical definition of functions. However, different set of inputs can give the same set of outputs! For example, different amounts of water varied as per different atmospheric humidity could produce the same quality of sunflower crops. In fact this is the key to optimization problems we will see in future posts.
Can we explore the above chain of thoughts on other day-to-day aspects? Examples:
- Function of a bicycle
- Ceiling fan
- Switch
- Smartphone