Why do we math? What is the role of math in our society, in our day-to-day lives? Even after using math in many ways, i don’t have a clear answer. I wonder why students would respond to these questions. It may be that there will be follwing responses:
- I don’t know.
- I like math, but i never thought of it as useful.
- It is used in economics and stock market and scientific research?
- Artificial Intelligence or data sciences?
- …
We might know instances where and when the tiger has been spotted, but we don’t know the tiger. So the question, why do we math?
To me, the pretext lies in humanity’s difficulty in dealing with uncertainty. If you don’t know when it will rain, you can’t sow your seeds because it will then be exposed to the birds and insects which might eat them up! Or how much time we could expect the sun to be in the sky? Or, how much of material which i need can i take in return for other materials which i have surplus? Imagine the early humans who began to worry about the uncertainties like the above. How would they deal with these, day in, day out. No one has the luxury to be born to a super rich family which ensures there are no uncertainties. In fact, the super rich worry about the uncertainty of their fortune and so are back in the same loop – how to make certain what is uncertain?
One core idea, which rests the human mind to a certain extent is that of patterns. Imagine a brick house, the bricks being the unit which was repeated in multiple ways to make the house. The idea that patterns exist in our world and the universe is so relieving! The sun’s time in the sky repeats day in day out. A known amount of grains give out a known amount of crops when planted. An object thrown up falls down, and that too if its thrown up in a certain fixed way, it falls down after a fixed time! This trick is the key.
With patterns, it may have been possible to the early humans to make simple this complicated scary world. They came to know that all these complications can be reduced to replications and combinations of smaller things. For example
house = x*bricks + y*cement + x*man-hours + other bits.
Now each thing, there could be seen as something to do with patterns which are repeated and combined with other patterns to make something complicated. Had this trickery not been discovered, there would be no brick houses. We would still be searching for a nice soft rock or twigs to make our nests. The implications of knowing or not knowing that patterns exist, could be severe. Can it be said that all knowledge is that of our eternal quest for patterns? Patterns we have discovered or perceive or are yet to discover?
But does a discovery of a pattern only have an emotional benefit aspect to it? No. We do something more – we make newer patterns from it for our other needs. A reference could be made here to an earlier blog post on Stereotyping Vs Prototyping that discusses our stereotyping tendency (fit everything into limited diversity of patterns). Making newer patterns, to add to our library of patterns, could be called as prototyping. We make models with a newly discovered pattern. When Newton and others came up with simplified mathematical form of the motions and bodies of the world, others rushed to use these simple representations of patterns to predict motion of astronomical objects, or for guessing the energy required to move objects vertically across a building and so on. So these patterns become models – tools which can be used.
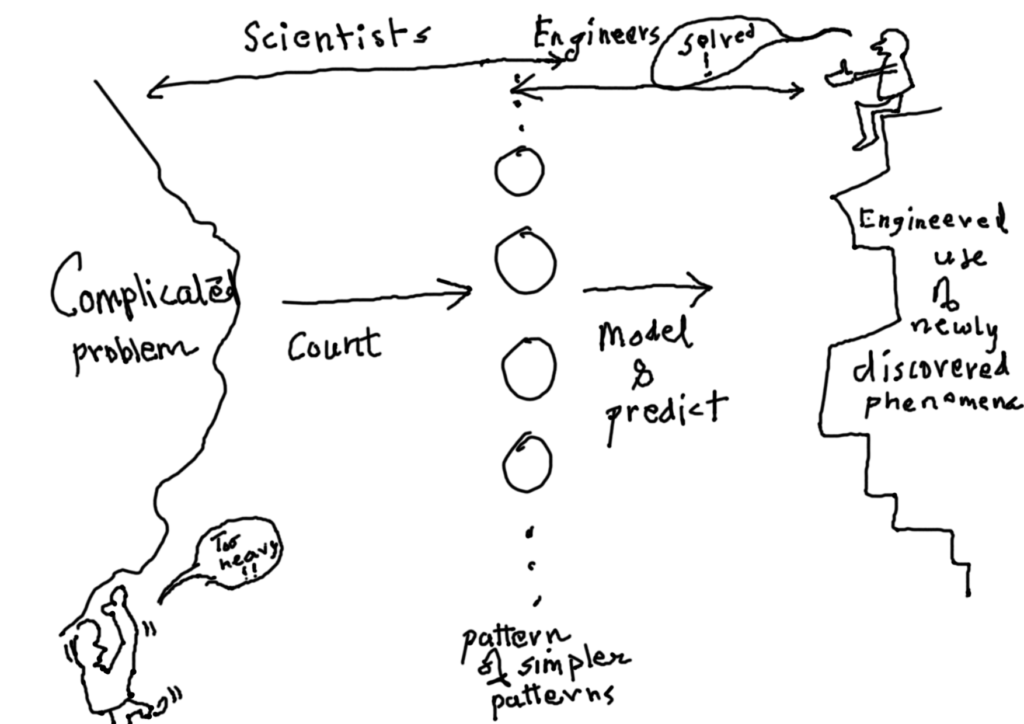
So what’s math got to do with all this pattern business? Well, math is basically counting. Why do we need to count and what is that? One way to put it is to account for something big and complicated by repeating something small and simple in so many counts. For example, you wish to move a table through a door. One way is to haul the heavy table and through trial and error see if it can get past the door with a few iterations. Another wiser way is to count the door dimensions as multiples of your palm width, and then do the same for the table. After you note these down, you can then simplify these further, and figure out which orientation of the table with respect to the door can achieve what you set out for. So the abstractification of the problem helps our mind to process, imagine, draw and basically manipulate known information (dimensions of the door and table) to illuminate the unknown (how to get one across the other). That is the essence of basic math.
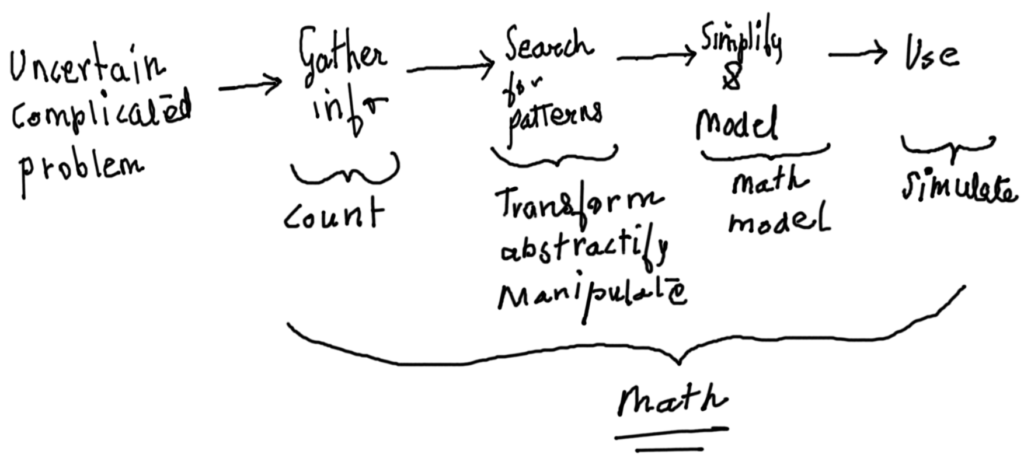
An example could be language. If someone’s speaking to you in sounds, how can you convert that into something you understand? So, typically you would record it – meaning count the intensity/volume of the person over a span of time. Then you would see if certain sound bytes correspond to the finger pointing of the person to certain fixed objects. This is searching for patterns. Then when you know say ‘debbidabbypoo’ corresponds to ‘run’ and ‘haletkaletpichkao’ corresponds to ‘You’ then you create a model sentence to test your interpretation on to the other person, something like ‘haletkaletpichkao debbidabbypoo’. This model will then be put on test and if the person runs away, you have a working model (and a lost sample)! But this is risky, you would like to learn first how to tell the person to come back before you ask it to run away. Now you see you are manipulating the situation to your benefit, also called taming the model. Similar things happen in all sorts of problems, and math is this tool that can help quantify, patternize, model, and simulate based on counting numbers and abstracting.